If you’ve ever had an optometrist dilate your eyes, you know that your pupils turn large and buggy. Creepy, right!?
Much like getting your eyes dilated, parent functions become bug-eyed too; that is… magnified in size! Did you know there are four main ways in which a parent function dilates? To help illustrate this process, think of a game controller like the one shown below. The green flashing buttons represent how a function can dilate on the x-axis while the purple flashing buttons represent how a function can dilate on the y-axis.
How do you dilate the function y = f(x) ?
Multiply ‘a’ to y = f(x) to become
y = af(x) or y = f(ax)
As you can see, you can multiply the function (the y-values) by a or you can multiply the inside of the function (the x-values) by a. Not only that, but you can choose the positive value of a by pressing the ‘+‘ or ‘–‘ buttons. If you press the ‘+‘ button, you make a bigger than 1 (like 2 or 450.9 or anything). If you press the ‘–‘ button, you make a smaller than 1 (like 0.25 or 0.50 or anything). As a result, pushing these flashing buttons create 4 combinations:
-
Y, a+
-
Y, a-
-
X, a+
-
X, a-
Y AXIS DILATION
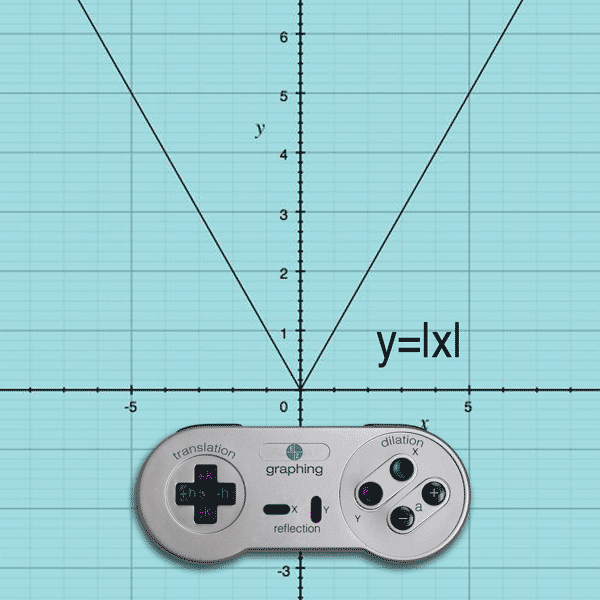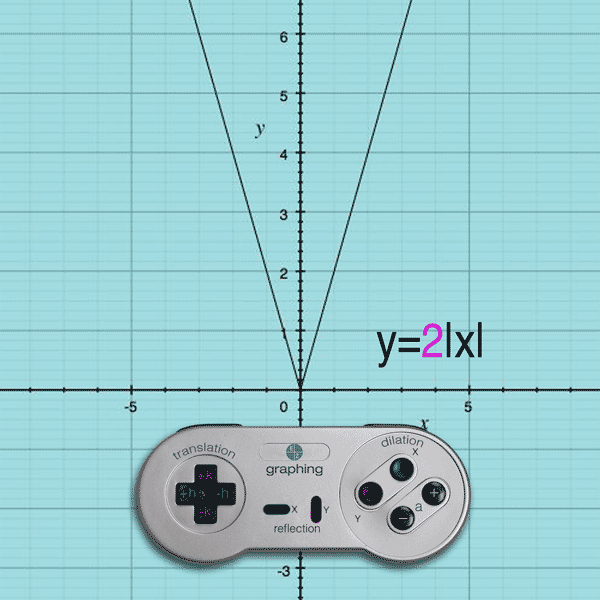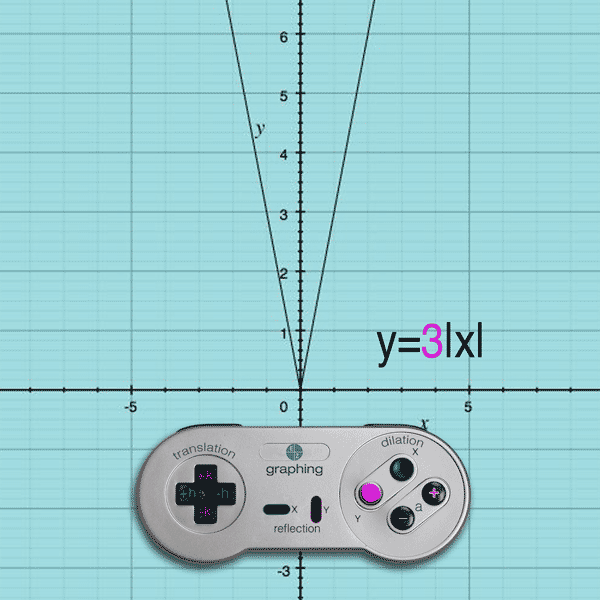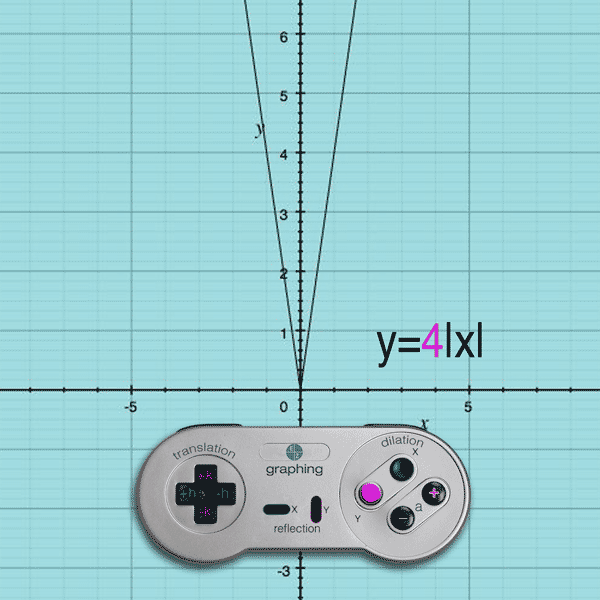
If you press the Y button and (+) button, the a value becomes greater than 1 and the result is a y-stretch
Example: y = 4|x| will stretch the y-values by a multiple of 4
(Note: Like Translations, the dilation effect on the y-values is exactly as you see it… multiplying by 4 multiplies the y-values by 4.)
If you press the Y button and (–) button, the a value becomes smaller than 1 and the result is a y-compression
Example: y = 1/4|x| will compress the y-values by a multiple of 1/4
(Note: Like Translations, the dilation effect on the y-values is exactly as you see it… multiplying by 1/4 multiplies the y-values by 1/4.)
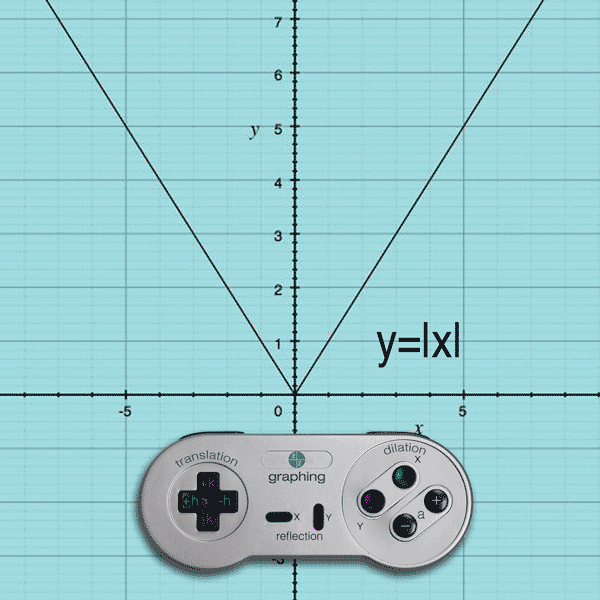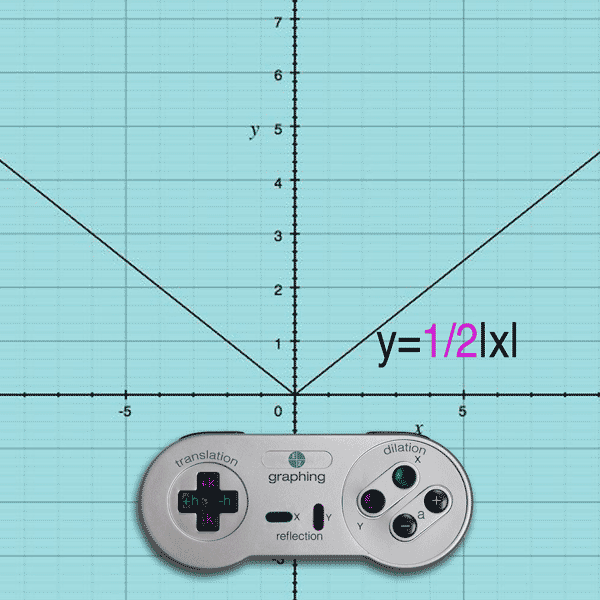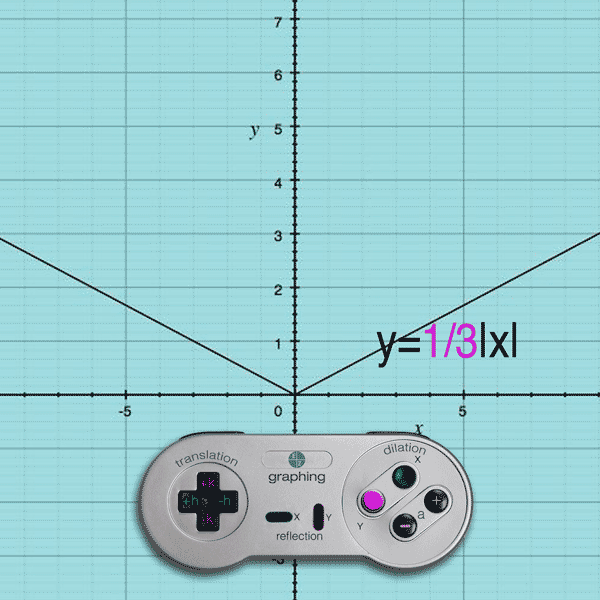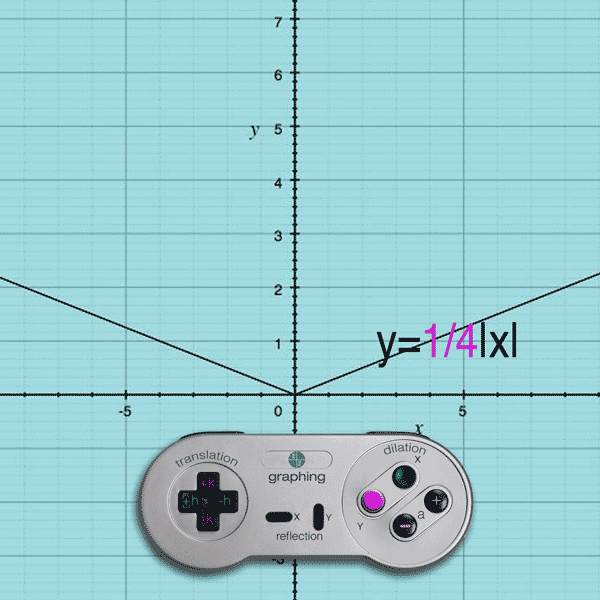
X AXIS DILATION
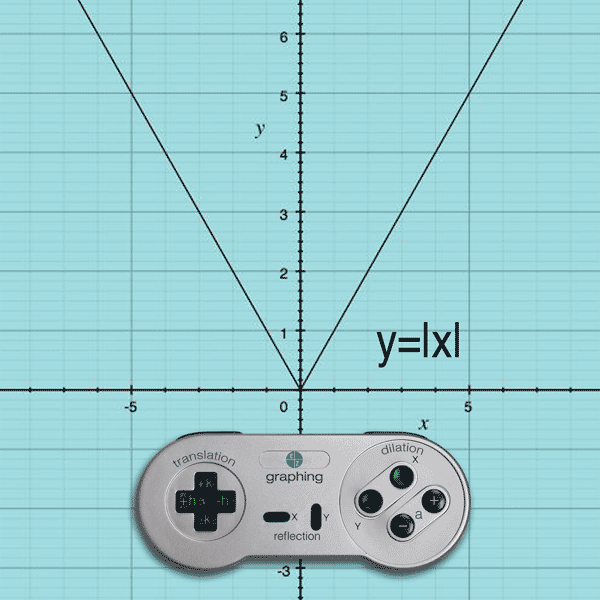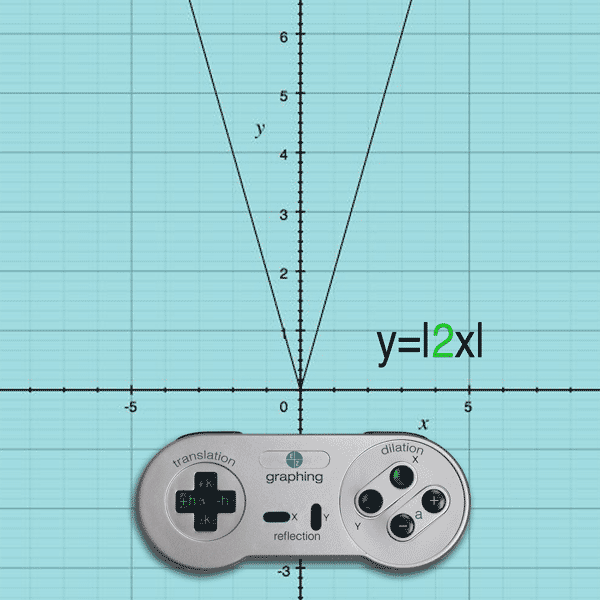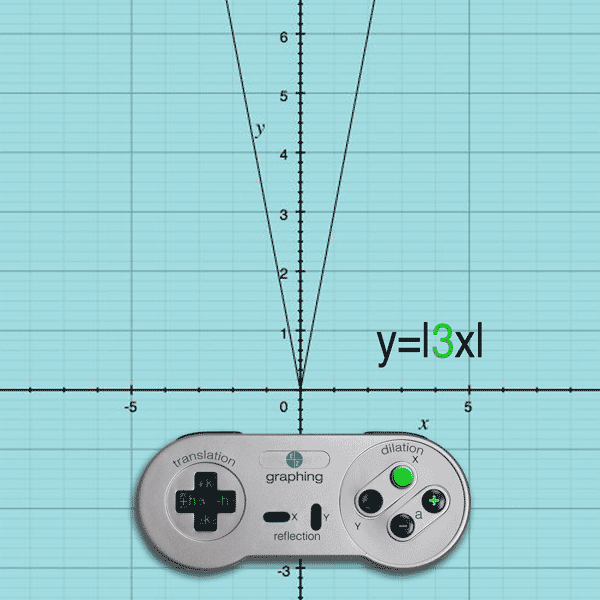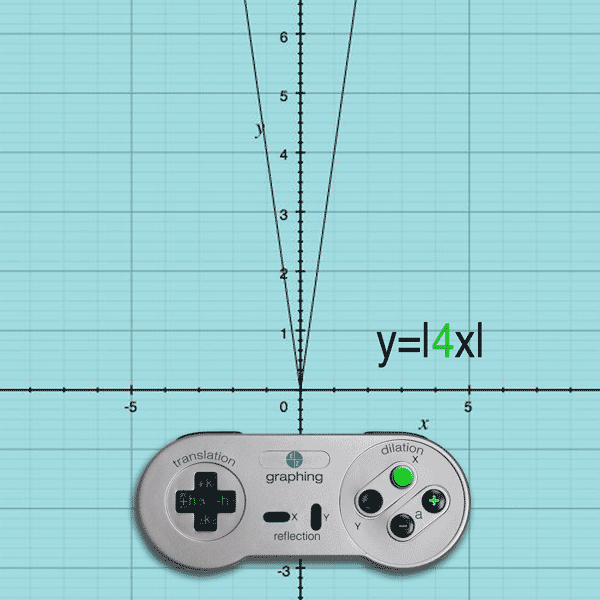
If you press the X button and (+) button, the a value becomes greater than 1 and the result is an x-compression
Example: y = |4x| will compress the original function by a value of 4 on the x-axis
(Note: Like Translations, the dilation effect on the x-values is opposite.)
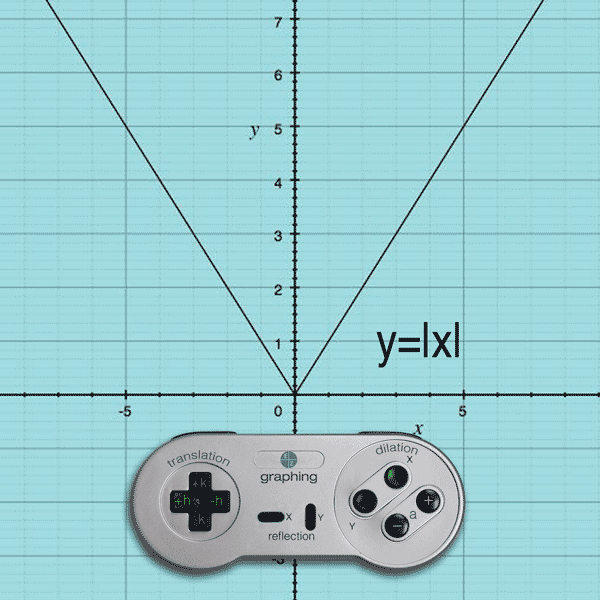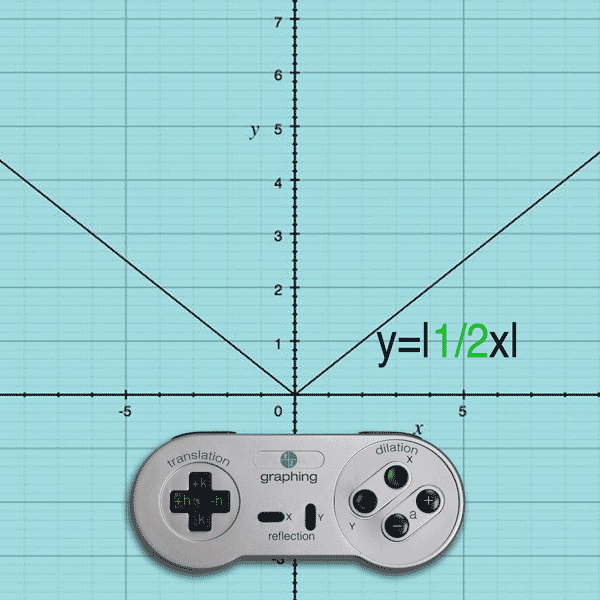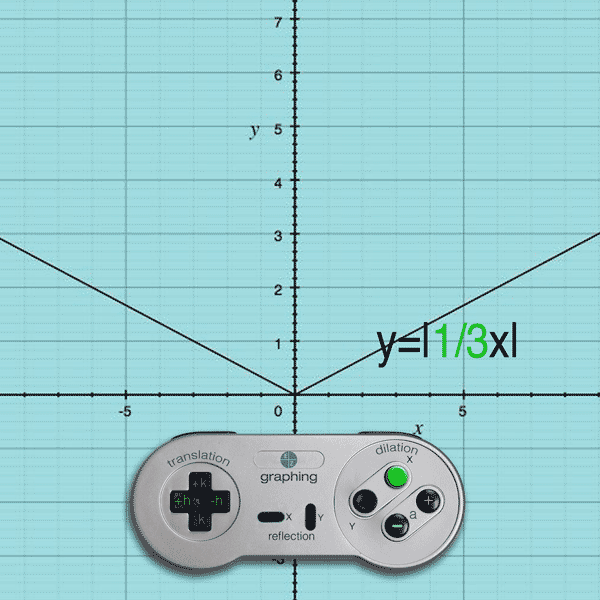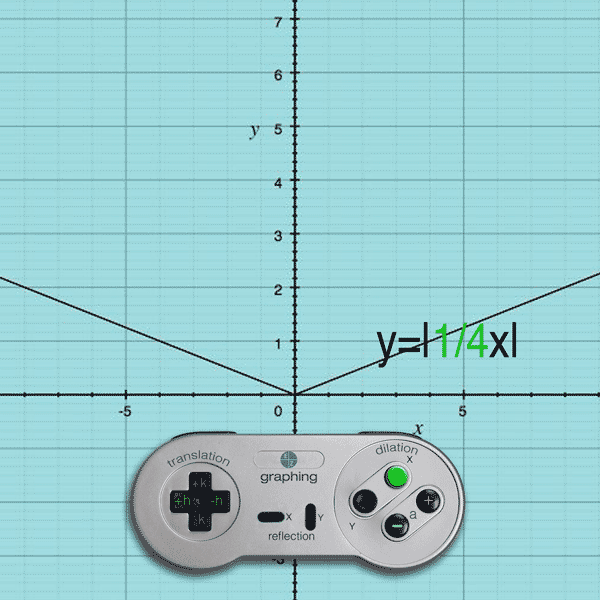
If you press the X button and (–) button, the a value becomes smaller than 1 and the result is an x-stretch
Example: y = |1/4x| will stretch the original function by 1/4 on the x-axis
(Note: Like Translations, the dilation effect on the x-values is opposite.)
Making the Connection
Hopefully you notice that there are four dilation combinations; however, there are two main ways a parent function can appear… tall or wide:
- A y-stretch can look like an x-compression (and vice versa). The functions appear taller than the original parent function. You should have also noticed that both of these dilations occur when ‘a‘ is increasing ‘+’.
- A y-compress can look like an x-stretch (and vice versa). The functions appear wider than the original parent function. You should have also noticed that both of these dilations occur when ‘a‘ is decreasing ‘-‘.